Shell Temperature Calculation
Once formed, a black shell has a surface
temperature determined by the energy of particles in its quanta. To
calculate this, the shell is assumed to have a Schwarzschild radius, rs,
determined by its mass, M. If G is the gravitational constant and c is
the speed of light,
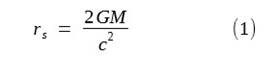
From this, the area of black shell’s event horizon,
As, is given by
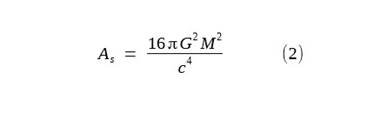
The mass collapsing into a black shell becomes
distributed uniformly throughout the quanta in the shell, maintaining
the inherent symmetry and simplicity of gravitationally collapsed
objects. The following equation provides the number of Planck areas, Np,
by dividing the shell area by the Planck area, Ap.
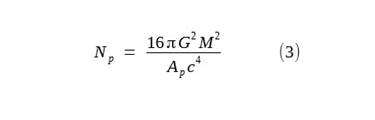
Ap is
not the area of the circular disk of a collapsed spacetime quantum. It
is the square of the Planck length, being the sum of the disk area plus
the average area of the dimensionless space between quanta. This square
tessellation of the shell surface determines the number of quanta
present.
Dividing the black shell mass by the number of
Planck areas provides the mass in each spacetime quantum, Mp.

Multiplying
the mass, Mp, by the square of the velocity of light provides the energy
per quantum of Planck area, Ep.

This mass per particle is difficult to attribute to
any particle other than a photon. A black shell five times the mass of
the sun’s has a particle mass of 3.79x10-46 kg. In comparison, a 1.1 eV
neutrino has a mass 1.78x10-36 kg.
In terms of universal constants
Ap is given by

The
energy per Planck area, Ep,
becomes

To obtain
the temperature, I assume the photons have only one degree of freedom.
Although each quantum has four contacts with other quanta,
movement of any photon in a two-dimensional symmetrically spherical
matrix of photons does not change the nature of the array. For the black
shell, all photons are identical.
The one degree of freedom left is that individual photons can
exchange spins in the spin-neutral array required to produce a uniform
shell surface. So, the
conversion factor for energy is
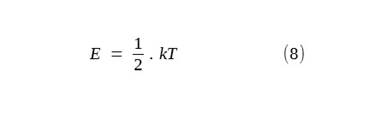
where T is the absolute temperature and k is the
Boltzmann constant.
The expression for temperature of the Planck area
and therefore that of the black shell, Tp, then becomes
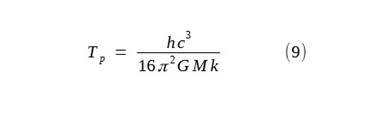
The
expression developed by Michael Hawkins for the temperature of a black
hole (12), T'p is

The two expressions are identical.
